Instalace rozšiřujících modulů
V základní nainstalované verzi prostředí NXT-G příliš podpory pro rozšiřující matematické funkce nenajdeme. V rámci modulu Math, který jsme si představili v předchozí kapitole, nalezneme pouze funkci absolutní hodnoty (Absolute Value) a druhé odmocniny (Square Root).
Pro goniometrické funkce je potřeba podporu nejprve doinstalovat. Návod na instalaci jednotek naleznete zde. Podporu pro goniometrické funkce sinus a kosinus a cyklometrickou funkci arcus tangens připravila firma HiTechnic. Rozšiřující blok HiTechnic Sin/Cos Math a HiTechnic ATan2 Math si můžete stáhnout z oficiálního webu výrobce či z těchto stránek (Sin/Cos, ATan2).
Rozcestník
Goniometrické operace můžeme využít díky bloku  HTSinCos. Ten je standardně umístěn v paletě
HTSinCos. Ten je standardně umístěn v paletě  Complete >
Complete >  Data, záleží však na instalaci.
Data, záleží však na instalaci.

Ten obsahuje jeden vstup # [Angle] určující úhel udávaný v radiánech či stupních a dva výstupy # [Sin(Angle)], vracející sinus zadaného úhlu a # [Cos(Angle)], vracející kosinus. Využít můžeme dle potřeby buďto jeden či oba výstupy.
Parametry bloku

Podle zvoleného typu jednotek (Units) bude blok vypočítávat sin a cos úhlu udaného buďto ve stupních (Degrees), nebo úhlu zadaného v radiánech (Radians).
Potřebujeme-li použít konkrétní předem danou hodnotu úhlu, nemusíme využívat konstanty, ale danou hodnotu můžeme doplnit do kolonky Angle (viz použití bloku Math).
Pomocí bloku  HTATan2 můžeme spočítat úhel odchylky polopřímky vycházející z počátku souřadnicového systému a procházející bodem X, Y s osou x. Pokud je úhel ve směru hodinových ručiček (nachází se pod osou x), bude kladný, pokud je proti směru (nachází se pod osou x), bude záporný. Podle nastavení jednotek (Units) bude pro stupně (Degrees) v rozsahu (-180; 180>, pro radiány (Radians) v rozsahu (-π; π>.
HTATan2 můžeme spočítat úhel odchylky polopřímky vycházející z počátku souřadnicového systému a procházející bodem X, Y s osou x. Pokud je úhel ve směru hodinových ručiček (nachází se pod osou x), bude kladný, pokud je proti směru (nachází se pod osou x), bude záporný. Podle nastavení jednotek (Units) bude pro stupně (Degrees) v rozsahu (-180; 180>, pro radiány (Radians) v rozsahu (-π; π>.
Blok je standardně umístěn v paletě  Complete >
Complete >  Data, záleží však na instalaci.
Data, záleží však na instalaci.

Ten obsahuje dva vstupy # X a # Y určující souřadnice bodu (viz výše) a jeden výstup # vracející úhel dle pravidel udávaný dle volby v radiánech či stupních.
Parametry bloku

Jednotky výstupu bloku (Units) lze zvolit buďto ve stupních (Degrees), nebo radiánech (Radians).
Vstupní hodnotami jsou data # X a # Y udávající souřadnice bodu jimiž prochází pomyslná polopřímka vycházející z počátku souřadnicového systému. Hodnoty lze buďto získat z externích připojených zdrojů či je můžeme přímo zadat jako parametr bloku.
Příkazy a metody
Podpora pokročilejších matematických funkcí je v jazyku RobotC o poznání komplexnější. V základní instalaci máme k dispozici celou řadu goniometrických a cyklometrických funkcí, nechybí ani absolutní hodnota, mocniny a druhá odmocnina.
Rozcestník
Goniometrické funkce
Goniometrické funkce lze v prostředí RobotC vypočítávat pro hodnoty úhlu zadaných ve stupních či v radiánech. Podle zvolené soustavy se liší i názvy jednotlivých příkazů.
Goniometrické funkce v radiánech
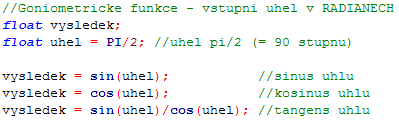
Funkce využívající základní syntax pracují s radiány. Jejich názvy jsou sin(úhel) a cos(úhel). Funkci tangens tg() mám programovací jazyk sice nenabízí, ale můžeme ji vypočíst jako výsledek podílu funkcí sin(úhel)/cos(úhel). Podívejme se na ukázku jejich použití:
Goniometrické funkce ve stupních
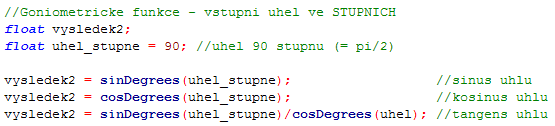
Potřebujeme-li vypočítat hodnoty pro úhly zadané ve stupních, použijeme funkce s alternativními názvy doplněné o Degrees, sinDegrees() a cosDegrees(). Zadání je pak následující:
Převod mezi stupni a radiány
Pomocí funkcí radiansToDegrees(hodnota) a degreesToRadians(hodnota) lze stupně a radiány převádět navzájem mezi sebou.

Goniometrické funkce ve výrazech
Goniometrické funkce (i ostatně jiné funkce) lze využít i přímo ve výpočtech matematických výrazů. V následujícím segmentu kódu vidíte využití funkcí sinus a kosinus pro výpočet souřadnic překážky zachycené radarem na displeji.

Cyklometrické funkce
I pro cyklometrické funkce nalezneme širokou podporu. Kromě funkce atan(hodnota) - arkus tanges, jíž lze rozšířit i prostředí NXT-G se v jazyce RobotC nachází arkus sinus asin(hodnota) a arkus kosinus acos(hodnota).
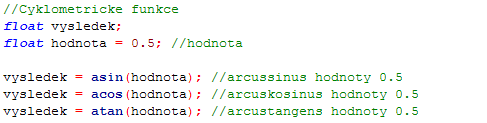
Speciální funkcí je funkce atan2(X,Y). Ta umožňuje spočítat úhel odchylky polopřímky vycházející z počátku souřadnicového systému a procházející bodem X, Y s osou x. Výsledný úhel je v radiánech a odpovídá funkci atan(Y/X).
Mocnina
Pro výpočet mocniny používáme funkci pow(base, exponent). Ta má dva parametry, prvním je základ (base) a druhým mocnina (exponent). Parametry odpovídají vztahu základmocnina (baseexponent). Potřebujeme-li tedy vypočítat 24, bude základem číslo 2 a mocninou číslo 4.
Ukázka použití druhé mocniny:

Ukázka použití n-té (4) mocniny:

Exponenciala se základem e
Pro výpočet hodnot exponencialy se základem e slouží funkce exp(mocnina). Ta odpovídá vyjádření emocnina.
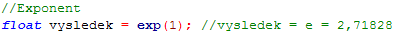
Odmocnina
Pro druhou odmocninu lze použít funkci sqrt(hodnota), viz ukázka.
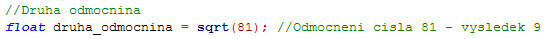
Zdálo by se, že tímto podpora odmocnin v prostředí končí a že např. 4. odmocninu již získat neumíme. Je nutno si ale uvědomit vztah mezi odmocninou a mocninou, kdy lze odmocnění realizovat jako umocnění převrácenou hodnotou (viz ukázka).

Logaritmy
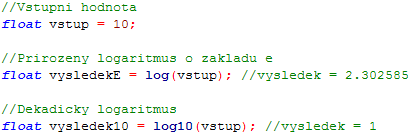
V prostředí RobotC můžeme pracovat s přirozenými i dekadickými logaritmy. Pro výpočet přirozeného logaritmu z čísla nám slouží funkce log(hodnota), pro dekadický logaritmus pak log10(hodnota).
Absolutní hodnota

Znaménko
Zajímavou funkcí je funkce sgn(hodnota). Ta nám vrací informaci, zda do ní vložené číslo je záporné (výstupní hodnota -1), nulové (výstupní hodnota 0) či kladné (výstupní hodnota 1). Využití této funkce může být např. u určení směru pohybu modelu, kdy nám tato funkce říká, zda je to směr vpřed, vzad či zda má model stát.
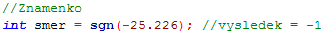
Import z knihovny funkcí
Pokud si nepamatujeme názvy klíčových slov vykonávajících matematické funkce, můžeme je nalézt v knihovně funkcí (Function Library) sekci Math.
Po přetažení položek v sekcích Commands do programového okna dojde ke vložení námi zvolené funkce.
![]() Random, který je umístěn v paletě
Random, který je umístěn v paletě ![]() Complete >
Complete > ![]() Data.
Data.
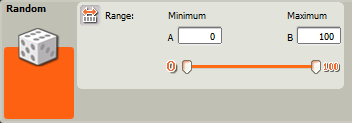
![]() Random obsahuje tři konektory pro propojení s dalšími bloky.
Random obsahuje tři konektory pro propojení s dalšími bloky.![]() A - spodní hodnota rozpětí čísel, ze kterých jsou generována náhodná čísla (možný rozsah 0 - 32767).
A - spodní hodnota rozpětí čísel, ze kterých jsou generována náhodná čísla (možný rozsah 0 - 32767).![]() B - horní hodnota rozpětí čísel, ze kterých jsou generována náhodná čísla (možný rozsah 0 - 32767).
B - horní hodnota rozpětí čísel, ze kterých jsou generována náhodná čísla (možný rozsah 0 - 32767).![]() Number - náhodně generované číslo z nadefinovaného rozpětí hodnot (mezi hodnotami A a B).
Number - náhodně generované číslo z nadefinovaného rozpětí hodnot (mezi hodnotami A a B).